tomobrien.vercel.app

Kinematics

We model robots as tree-like structures with a collection of rigid links, connected via joints.

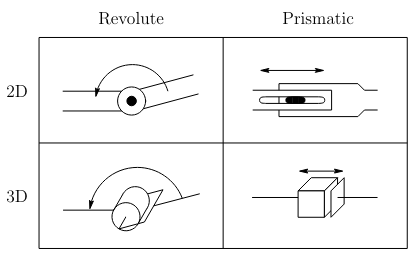
Joints

A joint allows a relative motion between the two links it interconnects, and is often modelled as either a revolute or prismatic joint. A revolute joint allows a relative rotation between the two links, while a prismatic joint allows a relative translation.

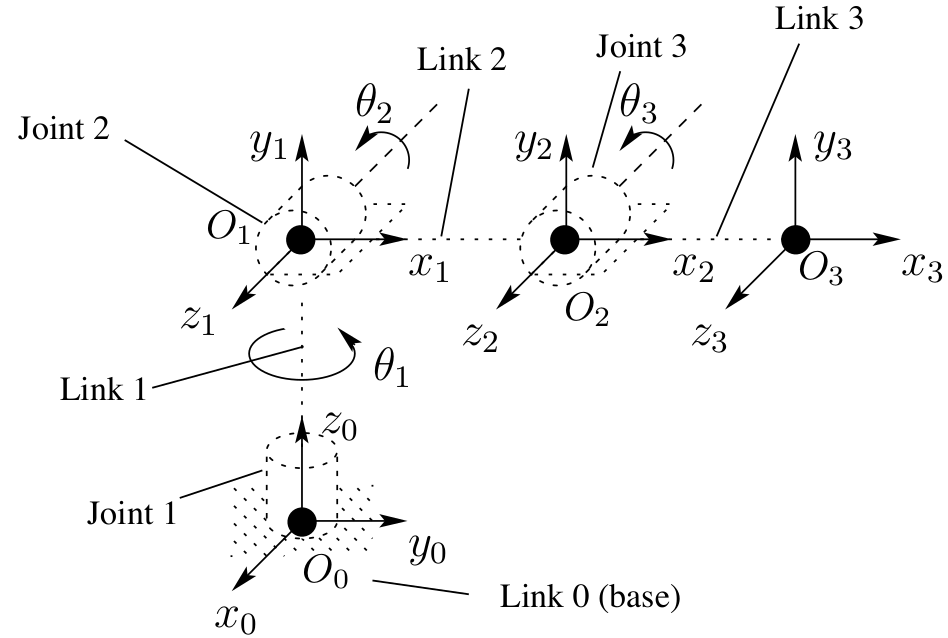
Forward Kinematics

The position of any link can be computed by the forward kinematics of the robot, which is a function of the joint angles. The forward kinematics for a serial chain robot is given by:

H_i^0(q)=H_1^0\left(q_1\right) H_2^1\left(q_2\right) \cdots H_n^{n-1}\left(q_n\right)=\left[\begin{array}{cc} R_n^0(q) & r_n^0(q) \\ \mathbf{0} & 1 \end{array}\right]

where $H_i^j(q)$ is the homogeneous transformation matrix from frame $0$ to frame $n$ along the robot's kinematic chain. Note, the forward kinematics of a non-serial chain robot is non-trivial to compute using the above equation but it must be ensured that the correct path is taken from the source to the target link in the kinematic chain.

Jacobian

The jacobian is a matrix which gives the relationship between the joint velocities and the linear and angular velocity of the robots end effector/point of interest.

v = J(q)\dot{q}\space

We can split the jacobian two parts, the linear velocity jacobian and the angular velocity jacobian:

J(q)=\begin{bmatrix} J_v\\J_w \end{bmatrix}

with

v^0_n=J_v(q)\dot{q} \\ \omega^0_n=J_w(q)\dot{q}

where $v^0_n$ and $\omega^0_n$ are the linear and angular velocity of the end effector/point of interest respectively, $J_v(q)$ and $J_w(q)$ are the linear and angular velocity jacobians respectively, and $\dot{q}$ is the joint velocity vector.

Computing the Jacobian

Computing the Jacobian is relatively simple, each column is related to a joint, the entries of the column depend on whether the joint is prismatic or revolute:

\textbf{J} =\begin{bmatrix} \textbf{J}_v\\ \textbf{J}_w \end{bmatrix} =\begin{bmatrix} \textbf{J}_{v1} && \textbf{J}_{v2} && \dots&& \textbf{J}_{vn}\\ \textbf{J}_{w1} && \textbf{J}_{w2} && \dots && \textbf{J}_{wn} \end{bmatrix}

\textbf{J} =\begin{bmatrix} \textbf{J}_{vi}\\ \textbf{J}_{wi}\end{bmatrix} = \begin{cases}\begin{bmatrix} z^0_{i-1}\\J_w \end{bmatrix} \text{for prismatic}\\ \\ \begin{bmatrix} S(z^0_{i-1})(r^0_{n/0}-r^0_{i-1/0})\\z^0_{i-1}\end{bmatrix} \text{for revolute} \end{cases}

z^0_{i-1}=R^0_1(q_1)R^1_2(q_2)\dots R^{i-2}_{i-1}(q_1)[0,0,1]^T